Con lắc thuận nghịch

Bao gồm:

- Con lắc thuận nghịch: Dài L = 120cm, khoảng cách 2 trục dao động (2 dao) là d = 80cm, trên con lắc được chia thành 25 vạch cách nhau 2.5cm. Có 2 gia trọng bằng đồng nặng 940g và 1360g. Có gá đỡ dao gắn lên tường. 

- Đồng hồ đo thời gian và cổng quang học. 

- Thước 30cm

Mục đích:

a. Xác định chu kỳ dao động T1, T2 của con lắc thuận nghịch

b. Điều chỉnh để chu kỳ T1 = T2

c. Xác định gia tốc trọng trường

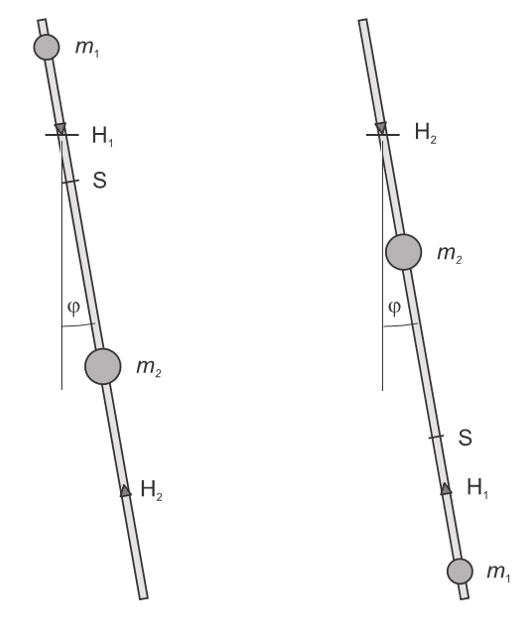
(Con lắc thuận nghịch)

Cơ sở lý thuyết:

Với một con lắc vật lý nói chung, khi nó dao động quanh 1 trục với góc lệch φ đủ nhỏ, ta có phương trình dao động:

                        (1)

Trong đó:

J: Mô men quán tính của con lắc đối với trục dao động.

s: Khoảng cách từ tâm vật nặng đến trục dao động

g: Gia tốc trọng trường.

m: khối lượng con lắc

Chiều dài rút gọn Sr của con lắc được định nghĩa bởi phương trình sau:

                                             (2)

Chu kỳ dao động của con lắc là:

                                          (3)

và lúc đó, con lắc vật lý được coi là một con lắc đơn có chiều dài Sr.

Theo lý thuyết trục song song, mô men quán tính của con lắc là:

                                    (4)

Trong đó: Js: là mô men quán tính của con lắc đối với trọng tâm con lắc.

Do đó:

                                       (5)

Với con lắc thuận nghịch.

Con lắc thuận nghịch là một loại của con lắc vật lý. Có 2 trục dao động H1 và H2. Hai gia trọng m1 = 940g và m2 = 1360g có thể dịch chuyển được. Do đó chu kỳ daao động thay đổi theo. Mục đích của việc làm thay đổi chu kỳ là để tìm vị trí mà hai chu kỳ thuận và nghịch bằng nhau.

Khi T1 = T2, lúc đó, chiều dài rút gọn của thuận và nghịch bằng nhau:

           (6)

s1 và s2 là khoảng cách từ tâm gia trọng đến trục dao động. Và:

                            (7)

Từ phương trình (6) và (7), xác định được:

                (8)

Nếu thế s1 vào s ở phương trình (5) ta được:

                                     (9)

Xác định gia tốc trọng trường bởi công thức:

                           (10)

Lắp đặt và Tiến hành thí nghiệm:

(Con lắc thuận nghịch)

• Như hình trên: Gắn con lắc vào tường để tránh rung, lắc.
• Gắn cổng quang vào tường (bằng ốc vít) sao cho thanh dao động cắt qua mắt quang học.
• Cố định gia trọng m1  = 1360g tại vị trí 10cm tính từ trục dao động (dao 1)
• Gia trọng m2 = 940g đặt ở vạch trên cùng cách dao 1 là x = 9.7cm

Đo chu kỳ dao động bằng 2 cách: 

+ Cách 1: Bật đồng hồ đo thời gian về Mode 4, đo trực tiếp chu kỳ dao động

+ Cách 2: Bật đồng hồ ở Mode 5: Đếm 50 chu kỳ hết bao nhiêu thời gian, rồi tính trung bình. 

Chúng tôi khuyến khích làm theo cách 2 để có độ chính xác cao hơn. 

• Kéo con lắc thuận nghịch khỏi vị trí cân bằng một góc nhỏ và thanh dao động che mắt của cổng quang và thả ra để con lắc dao động
• Đợi sau vài chu kỳ cho ổn định, ta ấn Start/Stop trên đồng hồ (Mode 5). Khi đồng hồ đếm đến 51 thì ấn Start/Stop một lần nữa để dừng lại, lúc này đồng hồ hiển thị thời gian của 50 chu kỳ. Ghi giá trị vào bảng số liệu.
• Dịch chuyển m2 xuống vạch tiếp theo. Và thực hiện đo như trên. Ta đo đến vạch cuối cùng là vạch 25. 
• Xoay trục dao động của lắc để chuyển sang đo chu kỳ thuận như hình dưới.

(Con lắc thuận nghịch)

• Giữ nguyên vị trí m1.
• Lại đo lần lượt như đo chu kỳ nghịch bên trên
• Bảng số liệu được lập dưới đây;

Vẽ đồ thị T₁² và T₂² phụ thuộc vào x₂ trên cùng một trục tọa độ.

Thấy rằng hai đồ thị cắt nhau ở 2 vị trí: 3.154 và 3.334

Từ phương trình (10) bên trên, ta tính được g1 = 10m/s2, g2 =  9.46m/s2

Vậy giá trị trung bình g = 9.73m/s2